L’algoritmo di Euclide permette di calcolare il massimo comun divisore, MCD, tra due numeri interi. Vedi Wikipedia: Algoritmo di Euclide.
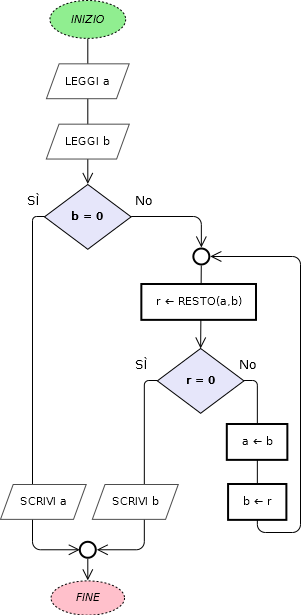 Algoritmo
Algoritmo
Dati due numeri naturali a e b
- se b è zero allora la risposta è a
- altrimenti si divide a per b e si assegna ad r il resto della divisione
- se r=0 allora la risposta è b
- altrimenti a ⇐ b e b ⇐ r e si ripete nuovamente la divisione.
Esempi
Con a=70, b=15
| a | b | r |
|---|---|---|
| 70 | 15 | 70=4*15 + 10 |
| 15 | 10 | 15=1*10 + 5 |
| 10 | 5 | 10=2*5 + 0, STOP |
MCD(70, 15)=5.
Con a=15, b=70
| a | b | r |
|---|---|---|
| 15 | 70 | 15=0*70 + 15 |
| 70 | 15 | … |
MCD(15, 70)=5.
Con a=71, b=15
| a | b | r |
|---|---|---|
| 71 | 15 | 71=4*15 + 11 |
| 15 | 11 | 15=1*11 + 4 |
| 11 | 4 | 11=2*4 + 3 |
| 4 | 3 | 4=1*3 + 1 |
| 3 | 1 | 3=3*1 + 0, STOP |
MCD(71, 15)=1.
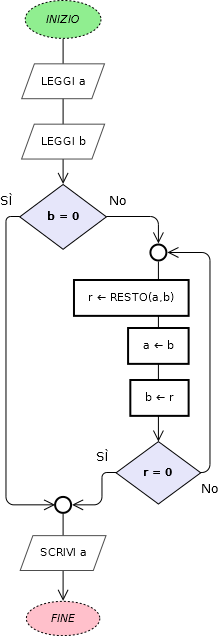 L’algoritmo precedente può essere trasformato in un programma di alto livello soltanto utilizzando l’istruzione GOTO.
L’algoritmo precedente può essere trasformato in un programma di alto livello soltanto utilizzando l’istruzione GOTO.
Con qualche modifica (le due assegnazioni vengono eseguite comunque) può essere adattato alla esigenze della programmazione strutturata.
Function euclide(a, b: Integer): Integer; Var r: Integer; Begin If(b = 0) Then euclide:=a Else Begin Repeat r:=a Mod b; a:=b; b:=r; Until(r = 0); euclide:=a; End; End;
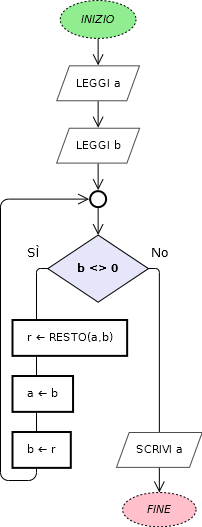 Con qualche altra modifica si semplifica ulteriormente il codice necessario
Con qualche altra modifica si semplifica ulteriormente il codice necessario
Dati due numeri naturali a e b
se b è diverso da 0
- r ⇐ resto della divisione intera tra a e b
- a ⇐ b
- b ⇐ r
- ripeti l’operazione
altrimenti
- la risposta è a
Esempio
Con a=70, b=15
| a | b | r |
|---|---|---|
| 70 | 15 | 70=4*15 + 10 |
| 15 | 10 | 15=1*10 + 5 |
| 10 | 5 | 10=2*5 + 0 |
| 5 | 0 | STOP |
MCD(70, 15)=5.
Function euclide(a, b: Integer): Integer; Var r: Integer; Begin While(b <> 0) Then Begin r:=a Mod b; a:=b; b:=r; End; euclide:=a; End;
Versione ricorsiva
Con a=70, b=15
MCD(70, 15) = MCD(15, 70 Mod 15)
= MCD(15, 10) = MCD(10, 15 Mod 10)
= MCD(10, 5) = MCD(5, 10 Mod 5)
= MCD(5, 0) = 5
= MCD(15, 10) = MCD(10, 15 Mod 10)
= MCD(10, 5) = MCD(5, 10 Mod 5)
= MCD(5, 0) = 5
Function euclide(a, b: Integer): Integer; Begin If(b <> 0) Then euclide:=euclide(b, a Mod b) Else euclide:=a; End;
oppure…
Function euclide(a, b: Integer): Integer; Begin If(b = 0) Then euclide:=a Else euclide:=euclide(b, a Mod b); End;