Algoritmo intuitivo e ottimo per le prestazioni.
Utilizza l’algoritmo di fusione di sottosequenze ordinate.
Procedure MERGESORT(Var V: Vettore; Inf, Sup: Integer);
Var
Medio: Integer;
Begin
If(Inf < Sup) Then
Begin
Medio:=(Inf+Sup) Div 2;
MERGESORT(V, Inf , Medio);
MERGESORT(V, Medio+1, Sup );
Merge(V, Inf, Medio, Sup);
End;
End;
...
MERGESORT(V, 1, N);
...
La chiamata chiede di ordinare l’array dal primo, 1, all’ultimo, N, elemento.
A ogni chiamata, dopo aver calcolato Medio, si effettuano due chiamate ricorsive, da Inf a Medio e da Medio+1 a Sup.
In pratica le chiamate ricorsive scendono fino al livello di array con un solo elemento.
Al ritorno di ogni coppia di chiamate si effettua la fusione, merge, delle due parti ordinate (l’array con un solo elemento è già ordinato…).
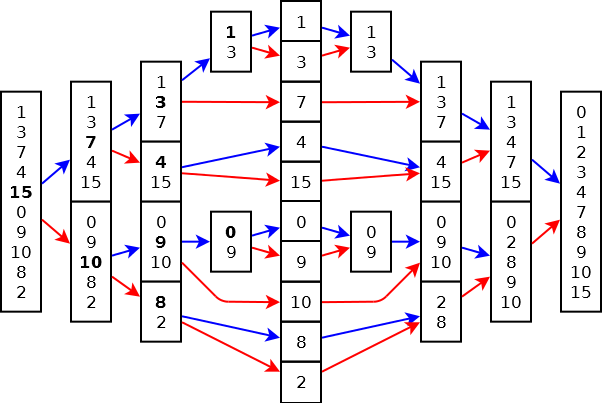
 Esempio 1
Esempio 1
Sia v={1, 3, 7, 4, 15, 0, 9, 10}
Le chiamate ricorsive sugli indici da 1 a 8 e con i valori medi successivi
- (1+8)/2 = 4
- (1+4)/2 = 2
- (5+8)/2 = 6
- (1+2)/2 = 1
- (3+4)/2 = 3
- (5+6)/2 = 5
- (7+8)/2 = 7
hanno l’effetto di raggiungere i singoli elementi.
Con i valori effettivi, l’array dopo le chiamate ricorsive diventa una sequenza di 8 array con un elemento
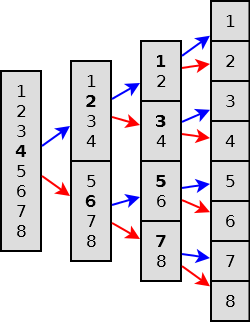
Al ritorno di ogni due chiamate ricorsive avviene la fusione di due array ordinati…
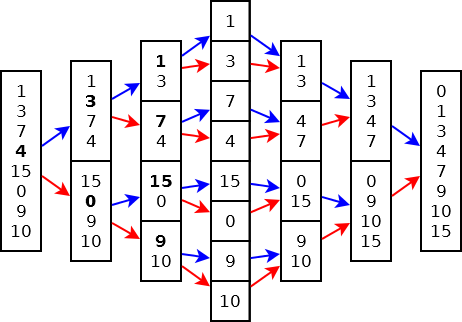
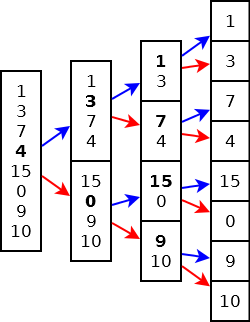
 Esempio 2
Esempio 2
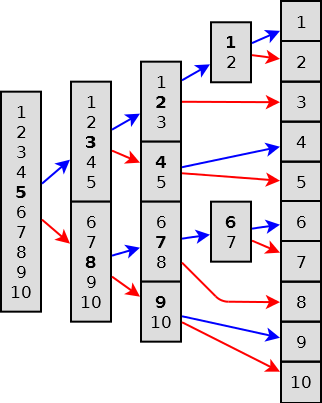
Sia v={1, 3, 7, 4, 15, 0, 9, 10, 8, 2}
Le chiamate ricorsive sugli indici da 1 a 10 raggiungono i singoli elementi con 2 passaggi in più…
- (1+10)/2 = 5
- (1+5)/2 = 3
- (6+10)/2 = 8
- (1+3)/2 = 2
- (4+5)/2 = 4
- (6+8)/2 = 7
- (9+10)/2 = 9
- (1+2)/2 = 1
- (6+7)/2 = 6.